导读：ENF试样裂纹尖端前的大规模纤维桥接是最常见的增韧机制之一，导致断裂韧性出现明显的阻力现象。为了考虑纤维桥接的增韧效应，准确模拟复合材料层合板的分层，提出了一种物理半解析方法，直接从实验载荷位移曲线出发，假设桥接为线性形式，确定II型桥接规律。该方法包括基于梁理论考虑纤维桥接引入闭合力的ENF试件的挠度分析和迭代确定桥接律参数的反方法。为了验证所提方法的有效性，将提出的方法识别出的桥接牵引力与传统内聚力律相结合，模拟了不同材料的单向层合板和多向层合板的整个分层传播过程。数值计算结果与实验结果吻合较好，说明了该方法的准确性和适用性。该方法的主要优点是减少了分层试验所需的指导，可作为研究试样分层行为的一种有效方法。

    纤维增强塑料(fiber reinforced Plastics, FRP)在航空航天、飞机等先进复合材料结构中得到了广泛的应用，具有高的比重比、优良的疲劳性能和降低制造成本等优点。但也存在许多局限性，如界面粘着力差、对缺陷敏感等，在各种加载条件下，容易引起相邻层间的分层。分层的发生会破坏结构的完整性，甚至导致复合材料结构在没有任何外部迹象的情况下发生灾难性破坏。在这三种基本的分层模式中，I型分层模式在过去的几十年里得到了充分的研究和讨论。同时，II型分层也具有重要意义，因为在工程实践中，许多复合材料结构通常受到弯曲荷载作用，导致分层在剪切模式下传播。因此，准确评估复合材料的II型分层行为对复合材料结构的设计至关重要。

    在这里，曹天成提出了一种基于梁理论的考虑纤维桥接效应的半解析方法，以线性桥接为假设，直接从实验载荷位移曲线出发，在II型分层模式下确定复合材料层合板的桥接牵引参数裂纹长度测量。加载点的挠度用外部载荷和桥接牵引参数解析表示，通过将实验和解析得出的挠度误差最小化，提出的优化方案可以识别这些参数。为了验证所提方法的准确性，分别采用了3种不同材料的单向层合板和文献中的多向层合板。在ABAQUS中，识别了桥接参数，并将桥接规律整合到三线性内聚规律中，模拟了ENF试件的整个分层过程。结果表明，该模型在所有工况下均能较好地预测整体荷载位移曲线，表明本文方法在确定ENF试件的II型桥接规律方面具有一定的准确性和适用性。目前的方法的优点是节省时间和成本效益。相关研究成果以题“An efficient semi-analytical method to extract the mode II bridging-traction law in ENF tests directly from the experimental load displacement data”发表在Composite Structures上。

    论文链接: https://www.sciencedirect.com/science/article/pii/S0263822322000423?via%3Dihub

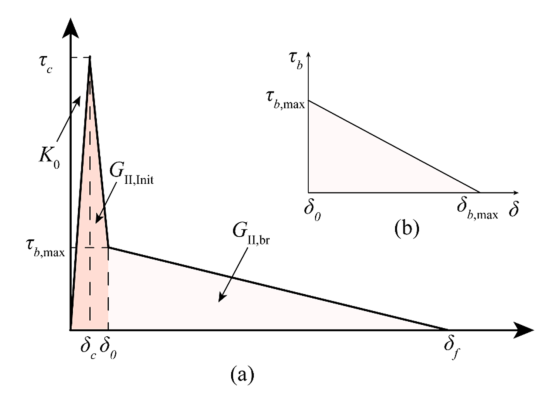
图1：桥接律的假设:(1)三线性内聚规律;(b)线性形式的桥接法则

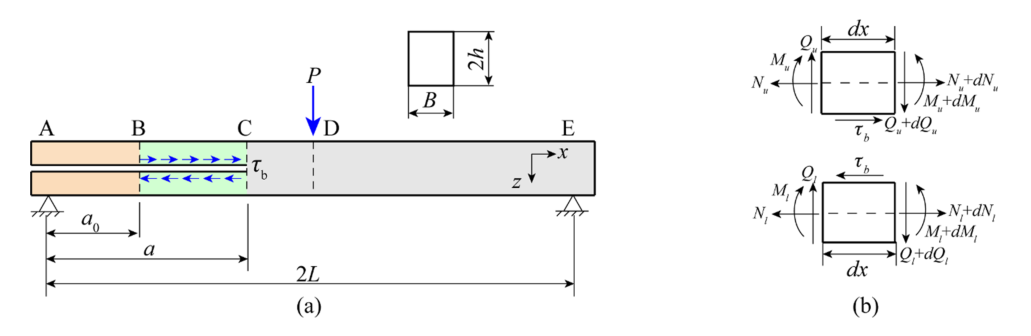
图2：ENF试样的几何和平衡条件:(a)几何条件;(b)平衡条件

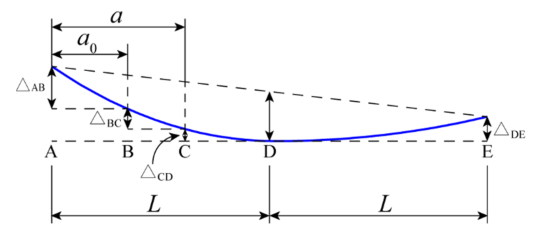
图3：ENF试样挠度的定义

图4： ENF试样起裂后的损伤演化与FPZ发展:(a)荷载位移曲线;(b)断裂韧性阻力曲线;(c)桥联律的损伤演变;(d)四个阶段对应的变形和FPZ发展

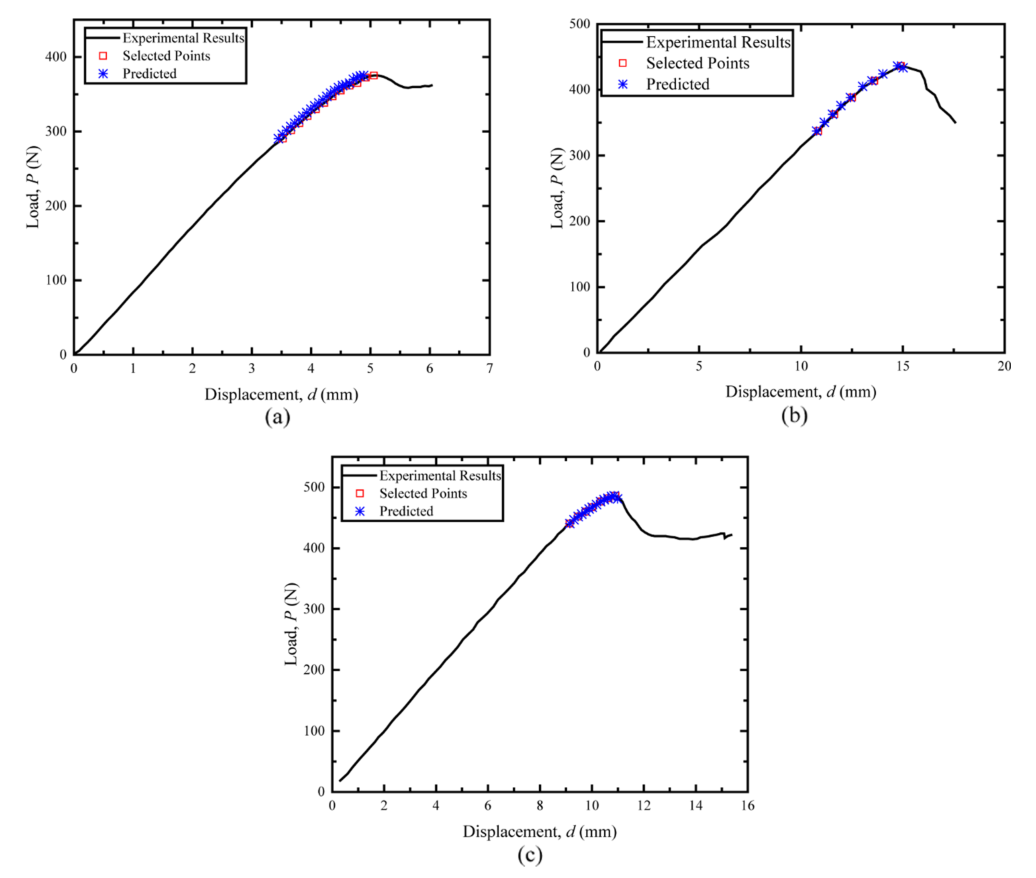
图5：试验荷载位移曲线及桥联律识别选定的点:(a)案例a;(b)案例b;(c) 案例c

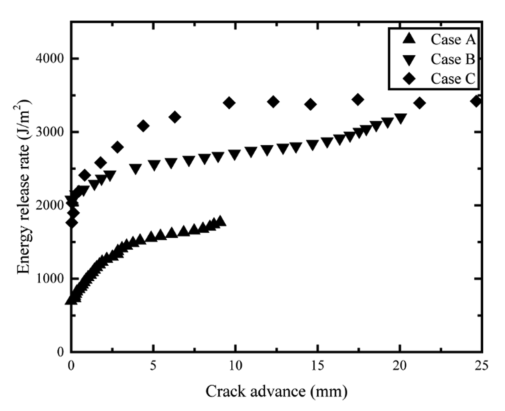
图6：三个模型的R曲线

图7：ENF试件的有限模型

图8：传统双线性形式

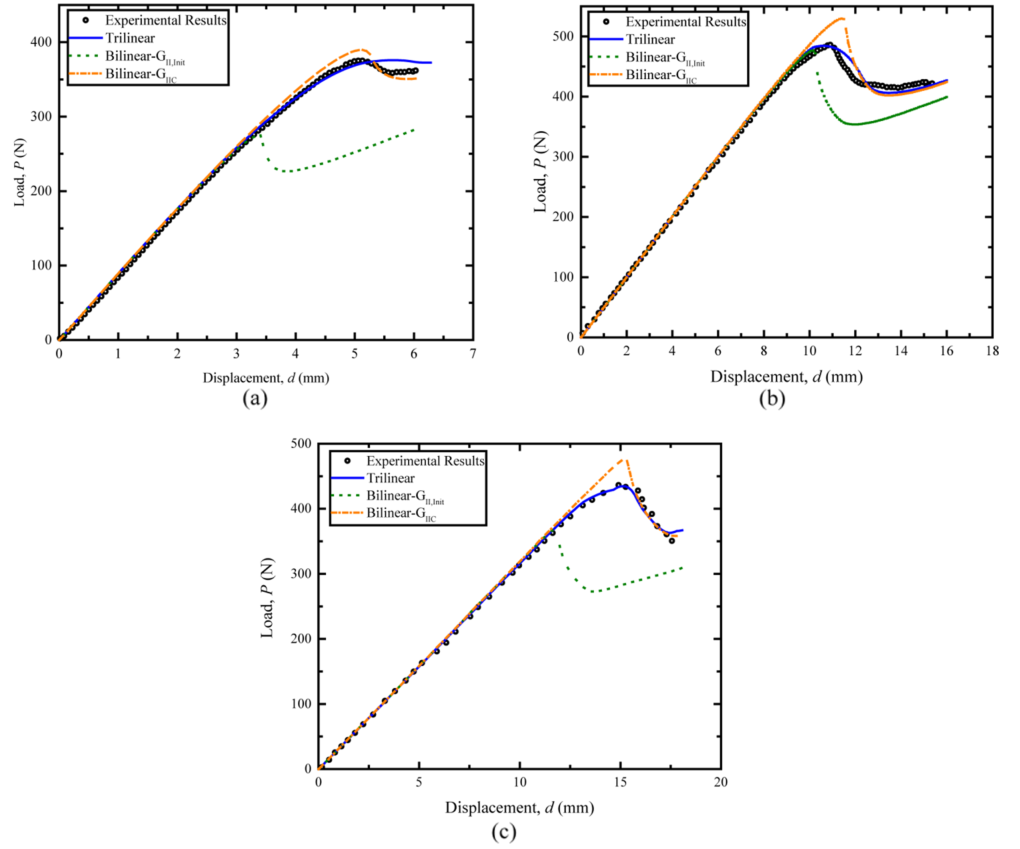
图9：荷载位移曲线数值结果与试验结果对比:(a)案例a;(b)案例b;(c) 案例c

    所提出确定II型桥接律的方法省时、成本低且不损失精度，并提出的有效的半解析方法，可直接从实验荷载位移曲线中提取复合材料层合板的II型桥接规律。这项工作是曹天成最近对模式I方法的扩展。该方法的准确性和适用性较好，具有极具意义的应用价值。